RUSALGO

ДО (дерево отрезков)

Необходимость

Зачастую необходимо отвечать на различные запросы на отрезках. Это может быть необходимым как просто при решении задачи, так и при непосредственном решении задачи с запросами.

Большое количество видов запросов можно выполнять за честные \(O(\log{n})\)

Это может быть запросы на:

  • сумму/минимум/максимум/НОД на отрезке
  • присвоение всех элементов какому-то числу
  • прибавление (умножение) на отрезке

    • И еще много всего интересного мы можем делать с небольшими хитростями.

    Сумма на отрезке

    Реализуем простую структуру, умеющую вычислять сумму на отрезке.

    Дерево отрезков - бинарное дерево, причем корень "отвечает" за всю последовательность, его дети за первую и вторую половину и так далее.

    То есть на каждом уровне длина отрезка уменьшается вдвое.

    Для лучшего понимания приведем пример: пусть дан массив \(p = \{1,2,3,4,5,6,7,8\}\)

    Составим ДО, где в вершине будет записана сумма подотрезка, за который отвечает эта вершина.

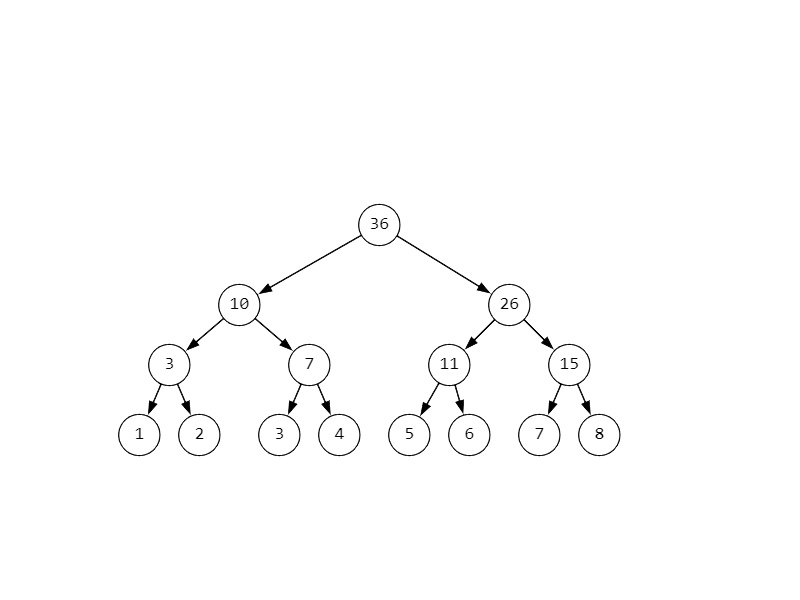
    Видно, что любая вершина является суммой двух ее потомков. Чтобы построить такое дерево можно воспользоваться простой рекурсией. 

    
ll tree[4*MAXN];
ll a[MAXN]; // данный массив

ll build(int v, int l, int r) {
  if(l > r) return 0; // неверный интервал
  if(l == r) return tree[w]=a[l]; // дошли до листа

  int med = (l+r)/2; // Считаем медиану
 
  ll leftQ = build(v*2, l, med); 
  // Левый ребенок отвечает за [l; med]
  ll rightQ = build(v*2+1, med+1, r);
  // Правый ребенок отвечает за [med+1; r]

  return tree[w] = (leftQ+rightQ);
  // Текущая вершина = сумма значений потомков
}

    Примечательны несколько моментов. Во-первых, можно показать что размер дерева линеен ( \(n+n/2+n/4...\) ). Во-вторых, мы получаем адрес потомков путем умножения адреса родителя на \(2\). Для правого потомка нужно прибавить \(1\).

    Теперь поймем, как находить сумму на отрезке \([l;r]\). Опять запустим рекурсию, будем поддерживать промежуток \([l_t,r_t]\). Тогда возможны три случая:

  • Текущий отрезок не пересекается с \([l;r]\). Тогда можно просто выйти из этой ветви рекурсии (мы можем вернуть \(0\) в случае с суммой на отрезке или \(+INF\) для минимума или \(-INF\) максимума).
  • Текущий отрезок пересекается с \([l;r]\). Тогда следует запуститься от потомков текущей вершины.
  • Текущий отрезок лежит внутри \([l;r]\). В этом случае можно просто вернуть значение текущей вершины. 
    • 
ll get_sum(int v, int l, int r, int ql, int qr) {
  // [ql;qr] - границы запрос 
  if( l > qr || r < ql || l > r ) return 0;
  if( l >= ql && r<= qr ) return tree[v];
  int med = (l+r)/2;
  return get_sum(v*2,l,med,ql,qr)+get_sum(v*2+1,med+1,r,ql,qr);
}

    Достаточно легко заметить, что мы можем опуститься до листа не более двух раз (правый и левый края запроса). Вполне очевидно, что сложность выполнения запроса не превышает \(O(\log{n})\), что и делает ДО такой уникальной структурой данных.

    Изменение в точке

    Давайте усложним задачу и допустим, что кроме запросов суммы (минимума/максимума) на отрезке существует еще запрос на изменение одного элемента. Формально говоря, запрос будет вида \((i,x)\), т.е. \(a_i:=x\).

    На самом деле, достаточно изменить лист и пересчитать значения во всех узлах, которые мы посетим (а их ровно \(\log{n}\)).

    
// a[p]:=x
void set_point(int v, int l, int r, int p,int x) {
  if(l==r){
    tree[v]=x;
    return;
  }
  int med = (l+r)/2;
  if(p <= med) set_point(v*2, l, med, p, x);
  else set_point(v*2+1, med+1, r, p, x);
  // здесь мог быть минимум или максимум:
  tree[v] = tree[v*2]+tree[v*2+1];
}

    Если все чем обременены - это изменение в точке и запросы на отрезке, то мы можем использовать ДО снизу, которое из-за особенностей построения позволяет избавиться от рекурсии и работает, конечно же, быстрее.

    Обновления на отрезке (массовые обновления).

    Усложним задачу. Необходимо выполнять два типа запросов:

  • сумма на отрезке
  • прибавление отрезке - \(a_l:=a_l+x, a_{l+1}:=a_{l+1}+x ... a_r:=a_r+x\)

    • Казалось бы, этого никак нельзя достичь. Но на помощь приходят ленивые вычисления.

    Давайте, когда нам приходит запрос на прибавление на отрезке, не будем посещать каждый лист, а только полностью лежащие внутри запроса узлы (как когда мы запрашиваем сумму на отрезке).

    Теперь запишем в специальный параметр (назовем его \(lazy[v]\)) тот факт, что на этом отрезке мы прибавили \(x\).

    И теперь, всякий раз посещая какую-либо вершину, мы будем проверять не прибавляли ли мы уже на этом отрезке, прибавлять к tree[v]+=(r-l+1)*lazy[v] и проталкивать в детей значение \(lazy[v]\).

    Таким образом, можно делать массовые обновление на отрезке.

    
int lazy[MAXN],tree[MAXN];

//обязательно выносим функцию, чтобы не загрязнять код ДО
//и не повторять одно и то же
inline void push(int w,int l,r) {
  if(l!=r) {
    lazy[2*w]+=lazy[w];
    lazy[2*w+1]+=lazy[w]; 
  }//делаем пуш в потомков
  tree[w]+=(r-l+1)*lazy[w];//прибавляем к каждому элементу
  lazy[w]=0;
}

// set a[i]+=v, nl <= i <= r
void upd(int w,int l,int r,int nl,int nr,int v) {
  push(w,l,r); //делаем пуш
  if(l>r d|| l > nr || r < nl) return;
  if(l>=nl && r<=nl) {
    lazy[w]=v;//присваиваем lazy
    push(w,l,r);//и сразу пушаем
    return;
  }
  int med=(l+r)/2;
  upd(w*2, l, med, nl,nr, v);
  upd(w*2+1, med+1, r, nl,nr, v);
  tree[w] = tree[w*2]+tree[w*2+1];
  //поддерживаем актуальное значение 
}
// функция суммы такая же, как без пушей,
// но так же делаем push в начале каждого вызова функции

    Модификации

    Модификации ДО (вроде MergeSort Tree или персистентное ДО) позволяют решать еще больший объем задач.

    Итоги

    ДО - невероятно мощная структура данных и ее использование очень широко. Часто оно играет второстепенную роль, спасая алгоритм из квадратичной асимптотики в \(n \log{n}\) (например ДП). Немало задач решаются сканлайном и деревом отрезков. Иногда достаточно просто подумать: "Мне нужна структура, которая умеет то-то за \(\log{n}\)", как в голову сразу приходит ДО.